IMD
Covalent Many-Body Potentials
IMD supports different types of many-body potentials for covalent materials, notably Tersoff potentials, Stillinger-Weber potentials, and Keating potentials. All these potentials are defined through analytic formulae, whose parameters are read from the parameter file. Stillinger-Weber type potentials can also be defined via tabulated parameter functions.
The three-body interactions of all covalent potentials are computed using neighbour tables. The initial length of a neighbour table can be specified with the parameter neigh_len, whose default value is 4. This is the typical number of neighbours in a covalent crystal. If necessary, the initial length of the neighbor tables is extended automatically. For the simulation of systems with more neighbors, such as liquids or amorphous systems, performance may improve if a higher initial neighbour table length is specified.
Tersoff Potential
The Tersoff potential (J. Tersoff, Phys. Rev. B 39, 5566 (1989)), which is enabled with the compilation option tersoff or tersoff2, is computed from its analytic expression, using parameters read from the parameter file. The Tersoff potential in its original form is enabled using the compilation option tersoff. It takes the following form:
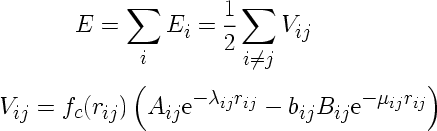
where
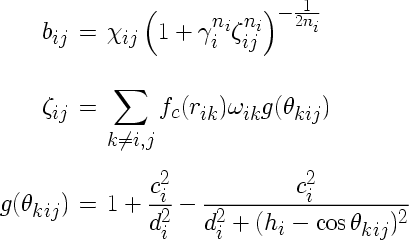
For the computation, the repulsive two-body part contained in this expression is computed from the parameters and filled into the corresponding potential table. Alternatively, it is possible to set the coupling constants Aij to zero, and use an arbitrary tabulated pair potential instead.
The cutoff function is also given analytically, by the following expression:
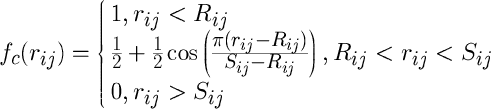
The Tersoff potential with a slightly different parameter structure is enabled using the compilation option tersoff2. In this case, the quantities bij and g have the following form:
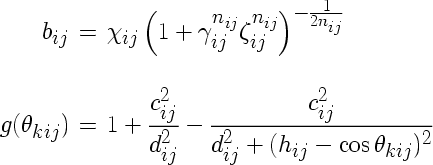
The indices of the parameters refer to atom types involved. The following IMD parameters correspond to the Tersoff potential parameters:
| tersoff | tersoff2 | |
|---|---|---|
| ters_a | A_ij | |
| ters_b | B_ij | |
| ters_la | lambda_ij | |
| ters_mu | mu_ij | |
| ters_ga | gamma_i | gamma_ij |
| ters_n | n_i | n_ij |
| ters_c | c_i | c_ij |
| ters_d | d_i | d_ij |
| ters_h | h_i | h_ij |
| ters_r_cut | S_ij | |
| ters_r0 | R_ij | |
| ters_chi | chi_ij | |
| ters_om | omega_ij | |
The values of the single-index parameters have to be given for all atom types in a row. The values of the two-index parameters except ters_chi and ters_om are read using the following format:
where n is the number of atom types. In the case of the variables ters_chi and ters_om, the diagonal values of the matrix are equal to 1 and the non-diagonal values are read using the following format:

The parameters ters_chi and ters_om are meaningful only if there is more than one atom type. They both default to 1 for all components. Note that the parameters ters_chi can be absorbed into the parameters ters_b, in which case the default values for ters_chi can be used.
Modified Tersoff Potential
The modified angular-dependent term b (T. Kumagai et al, Comput. Mater. Sci. 39, 457 (2006)) is enabled using the compilation option tersoffmod or tersoffmod2. The function form is as follows:
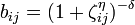
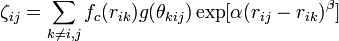
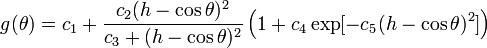
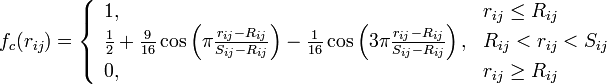
The following IMD parameters are relevant for the modified Tersoff potential:
| tersoffmod | tersoffmod2 | |
|---|---|---|
| ters_a | A_ij | |
| ters_b | B_ij | |
| ters_la | lambda_ij | |
| ters_mu | mu_ij | |
| ters_eta | eta_i | eta_ij |
| ters_delta | delta_i | delta_ij |
| ters_alpha | alpha_i | alpha_ij |
| ters_beta | beta_i | beta_ij |
| ters_c1 | c1_i | c1_ij |
| ters_c2 | c2_i | c2_ij |
| ters_c3 | c3_i | c3_ij |
| ters_c4 | c4_i | c4_ij |
| ters_c5 | c5_i | c5_ij |
| ters_h | h_i | h_ij |
| ters_r_cut | S_ij | |
| ters_r0 | R_ij | |
Stillinger-Weber Potential (analytic)
The Stillinger-Weber potential (F. H. Stillinger and T. A. Weber, Phys. Rev. B 31, 5262 (1985)) computed from its analytic formula is enabled with the compilation option stiweb. Note that there is is also the possibility to define potentials of this type by tabulated parameter functions, using the compilation option ttbp.
The Stillinger-Weber potential is given by
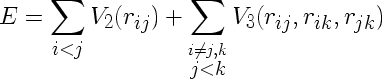
where V2 and V3 are given by
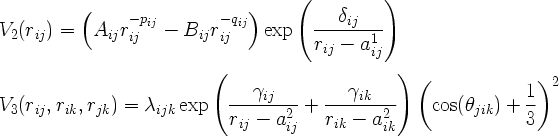
The angle theta_jik is the bond angle between the bonds ij and ik. V2 and V3 are zero for rij larger or equal to a1ij and a2ij, respectively. The following IMD parameters correspond to the potential parameters:
| stiweb_a | A_ij |
| stiweb_b | B_ij |
| stiweb_p | p_ij |
| stiweb_q | q_ij |
| stiweb_de | delta_ij |
| stiweb_a1 | a1_ij |
| stiweb_ga | gamma_ij |
| stiweb_a2 | a2_ij |
| stiweb_la | lamda_ijk |
The values of the two-index parameters have to be given for all atom types in the following format:
where n is the number of atom types. In the case of stiweb_la, the first index runs from 0 to n-1, whereas the last two indices are expected like for the two-index parameters.
Zhou-Wadley Potential (analytic)
The Zhou-Wadley potential (X. W. Zhou and H. N. G. Wadley, monatomic in Comp. Mat. Sci. 39, 340 (2007) and diatomic in Comp. Mat. Sci. 39, 541 (2007)) is a generalization of the Stillinger-Weber potentials for bcc and zinkblende structures. The computation from its analytic formula is enabled with the compilation option ternbcc. Note that there is is also the possibility to define potentials of this type by tabulated parameter functions, using the compilation option ttbp together with xt.
The parameters are the same as those for the Stillinger-Weber potential (analytic).
Stillinger-Weber Potential (tabulated)
Using the compilation option ttbp (two- and three-body potentials), it is also possible to specify Stillinger-Weber type potentials with tabulated parameter functions.
The two-body part is then treated as any other short range pair potential, and can be specified independently of the three-body term. It is usually read from from the potential file specified by the parameter potfile, but one could use also one of the analytically defined potentials.
The three-body term takes the following general form:
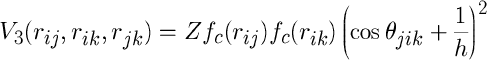
Z is the force constant and fc (r) is a cutoff function. The parameter h indicates the hybridization sph of the atoms. In the case h=3 the coordination is fourfold, whereas in the case h=2 the coordination is threefold.
The cutoff function fc (r) must be given in tabulated form, and is read from the file specified by the parameter ttbp_potfile. The parameter ttbp_constant specifies the force constant Z, and the parameter ttbp_sp the hybridization constant h.
Zhou-Wadley Potential (tabulated)
Using the compilation options ttbp and xt (two- and three-body potentials extended), it is also possible to specify Zhou-Wadley type potentials with tabulated parameter functions.
The parameters are the same as those for the Stillinger-Weber potential (tabulated).
Keating Potential
The Keating potential (P. N. Keating, Phys. Rev. 145, 637 (1966)), which is enabled in IMD with the compilation option keating, was one of the first many-body potentials for covalent systems. It is suitable only for small displacements from the ideal positions, and therefore mainly of historic interest. In particular, it should not be used for disordered systems.
The Keating potential, whose parameters have to be specified in the parameter file, takes the following form:
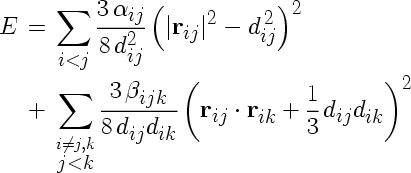
where the sums are over atoms i and nearest neighbour atoms j,k with distance vectors rij and rik. The parameters dij are the equilibrium distances between the atoms. They have to be specified in the IMD parameter keating_d. The values of these parameters have to be given for all pairs of atom types in the following format:
Here, n is the number of atom types.
The IMD parameters keating_alpha and keating_beta correspond to the force constants alpha_ij and beta_ij. keating_alpha has to be given in the same format as keating_d. For keating_beta, the index i runs from 0 to n-1, whereas the other two indices are read in like the two-index parameters.
The IMD parameter keating_r_cut corresponds to a cutoff length for all pairs of atom types. It is used to determine the nearest neighbour atoms. The format of keating_r_cut is the same as for keating_d.